Stats for Dummies - Episodio 1: La Media
La seconda rubrica curata da Luca Cappelletti si chiamerà, appunto, Stats for Dummies. Il primo articolo parla della media (“La media è un singolo valore numerico che descrive sinteticamente un insieme di dati”)

Le statistiche hanno sempre fatto parte del basket. Punti, rimbalzi, assist e molti altri contributi sono da sempre contabilizzati durante le partite, alcuni per il normale scorrere del gioco (punti, falli), altri per determinare l’apporto dei giocatori alla squadra (assist, stoppate).
Negli ultimi anni però si sono diffuse sempre più le cosiddette statistiche avanzate, ovvero numeri che richiedono alcuni passaggi matematici per ottenerle, ma che consentono di avere una visione più chiara su partite, squadre e giocatori. Parte degli amanti del basket però sembra avere una certa diffidenza nei confronti di quest’ultime.
Questa rubrica, Stats for dummies, cercherà di spiegare tutto ciò che c’è dietro i numeri e il loro utilizzo nel mondo del basket, al fine di smentire questa diffidenza che aleggia attorno ad esse. Alla fine le statistiche altro non sono che strumenti e, come tali, possono essere usate bene o male; tutto sta nella conoscenza dello strumento stesso.
In questa prima puntata partiamo da un concetto basilare, ma quanto mai importante, per comprendere le statistiche: la media.
Tutti noi usiamo le medie, nel basket, come nel quotidiano. Eppure, capita non di rado di imbattersi in errori grossolani. Andiamo con ordine e recuperiamo la definizione di media da Wikipedia:
“La media è un singolo valore numerico che descrive sinteticamente un insieme di dati”
In altre parole tramite la media riassumiamo in un unico valore un insieme di dati. Piuttosto che elencare i punti realizzati in ogni partita da un giocatore, si calcola la media per concentrare quell’elenco in una unica cifra. Tutto ciò è comodo, ma nasconde delle insidie.
Infatti quasi inconsciamente ogni volta che leggiamo delle medie buttiamo un occhio sul numero di partite giocate. Perché? Il motivo è facilmente intuibile: il solo valore della media non ci permette di avere una chiara idea di come quel giocatore o squadra abbia ottenuto quella cifra.
Prendiamo un esempio pratico: nell’ultima stagione, Khris Middleton ha mediato 20,1 punti a partita. Marshon Brooks la stessa identica cifra. Tralasciando le sensazioni che questi due nomi possono dare, è chiaro che la prima cosa da fare è controllare il numero di gare giocate: 82 per l’ala di Milwaukee, 7 per l’ex Olimpia Milano. Una bella differenza, trascurando anche il fatto che il secondo avrà giocato partite di poca o nulla importanza.
Questo aspetto delle partite giocate non è riscontrabile leggendo la sola media: i punti realizzati in ogni partita dai due americani portano ad avere la stessa media di punti, ma quest’ultima è stata ottenuta con percorsi nettamente differenti. Spesso si dice che i numeri non mentono mai: questo è un esempio calzante. Le due medie non mentono, sta al lettore capire che Brooks probabilmente non riuscirebbe a garantire quell’apporto di punti alla squadra se giocasse quanto Middleton. Alle volte tutto ciò è trascurato: si confrontano medie di giocatori con partite giocate (o minuti di utilizzo) totalmente differenti, parificando contributi che equivalenti proprio non sono. Si trascura quindi la “storia” della media e ciò può portare a considerazioni sbagliate.
Il controllo del campione (ovvero il numero di elementi su cui è stata calcolata la media) è uno strumento basilare nel mondo della statistica: una media calcolata su un campione ristretto è una media poco attendibile da cui solitamente si diffida.
Un altro strumento basilare nel mondo della statistica è la deviazione standard: senza entrare troppo nel mondo teorico, grazie ad essa si possono ottenere informazioni che la sola media non dà.
Facciamo un nuovo esempio: nell’ultima regular season Atlanta, Orlando e Miami hanno mediato gli stessi punti a partita, ovvero 103,4. In questo caso il campione è lo stesso per tutte e le squadre in analisi, ovvero 82 partite giocate. Seppur quindi le medie siano calcolate su campioni uguali, non ci permettono di capire come le tre squadre abbiamo raggiunto quella cifra. Per avere qualche informazione in più potrei confrontare i punti segnati ad ogni partita: 82 valori per 3 squadre sono quasi 250 numeri da confrontare. Decisamente troppi, ma in nostro soccorso viene appunto la deviazione standard. Questo strumento statistico ci permette di conoscere il discostamento medio del singolo valore rispetto alla media. Il grafico qua sotto aiuterà sicuramente a comprendere meglio il tutto: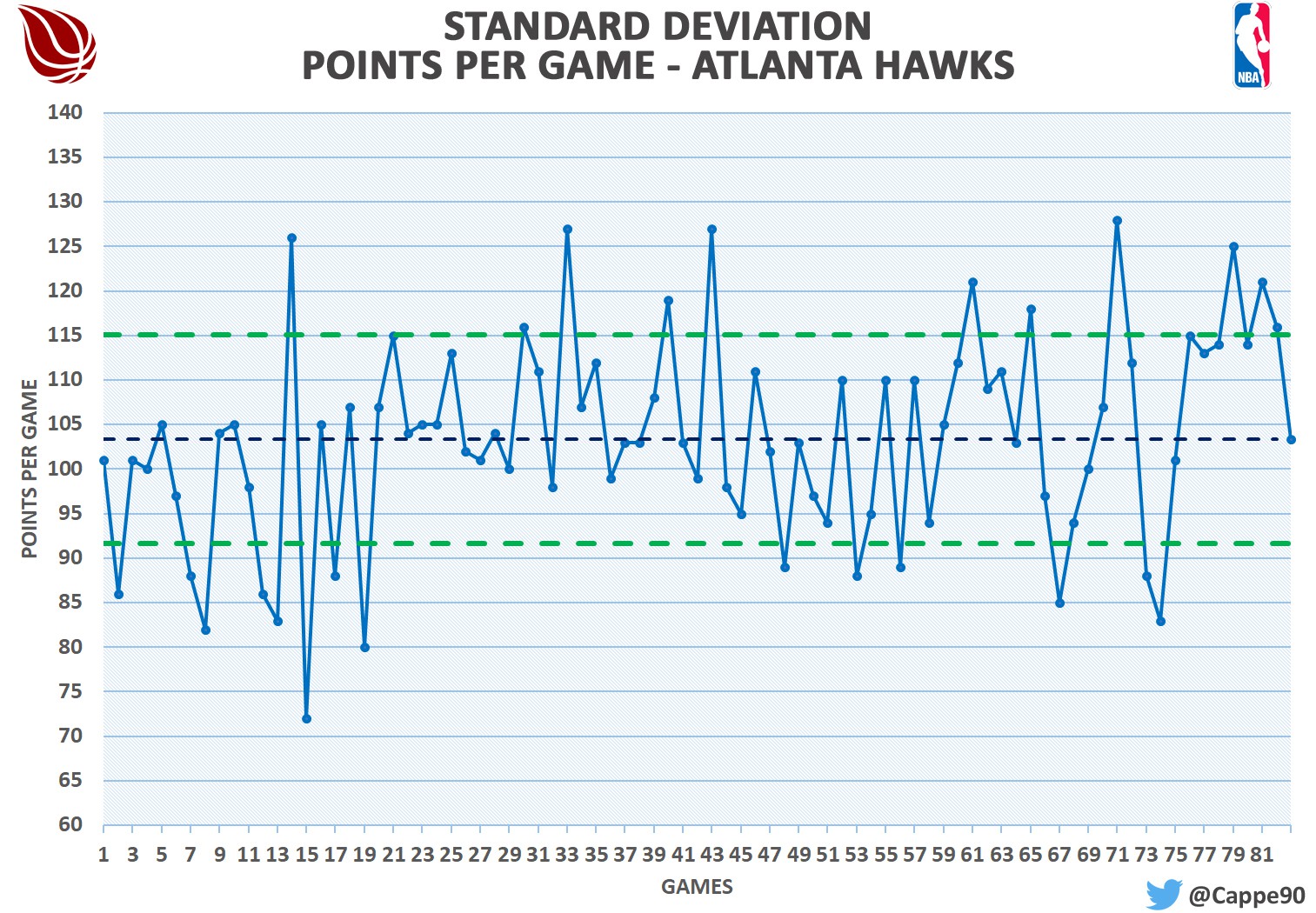
La linea blu mostra l’andamento partita per partita di Atlanta; la linea blu tratteggiata è invece la media. Le due linee verdi tratteggiate invece distano di una stessa misura dalla linea della media: tale distanza è la deviazione standard. All’interno di quella zona vi sono la maggior parte dei risultati ottenuti da Atlanta. In altri termini, durante la regular season gli Hawks segnavano molto probabilmente dai 92 ai 115 punti. Per Miami l’oscillazione è praticamente identica a quella di Atlanta, mentre per Orlando varia tra i 94 e i 113. Ok, differenze minime, ma potete immaginare comunque l’importanza della deviazione standard: leggendo le sole medie non potremo avere subito chiaro che è Orlando la squadra più costante tra le tre nel segnare i famosi 103,4 punti.
In Europa la deviazione standard è uno strumento che ha ancora più rilevanza rispetto agli USA: questo perché il numero medio di partite che si giocano ad est dell’Atlantico è di molto inferiore alla NBA; solitamente ci aggiriamo attorno alle 30 partite stagionali contro le 82 americane.
Come abbiamo scoperto prima, una media che si basa su un campione ristretto è meno solida. Ma perché lo si dice? Perché il singolo valore “anomalo” (di molto maggiore o minore rispetto agli altri che compongono il campione) incide molto di più su una media con larghezza del campione ristretta. Esempio molto assurdo per rendere l’idea: un giocatore segna sempre 20 punti, ma in una partita ne mette a referto 50. Nel caso abbia giocato dieci partite la media complessiva sarà 23, mentre se ne gioca 40 la media sarà 20,8. Quella singola partita da 50 punti incide molto di più sul primo campione che sul secondo.
Quando quindi abbiamo a che fare con campioni ridotti (come nel caso di campionati europei) la deviazione standard permette di comprendere meglio il modo in cui quella media è stata ottenuta.
Ulteriore esempio: Gudaitis di Milano e Kennedy di Pistoia hanno mediato nell’ultima stagione gli stessi punti, ovvero 10,9. Queste due medie scaturiscono da prestazioni ben differenti. Nelle otto partite giocate da Kennedy c’è una singola prestazione da 26 punti: questa partita porta la media da 8,7 alla nota 10,9. In termini di deviazione standard si passa da un valore di 5 punti per Arturas ai 6,3 per l’ala pistoiese. Grazie alla deviazione comprendiamo immediatamente che il lungo lituano è stato più costante di Kennedy, mentre il secondo ha beneficiato di una singola partita per avere una media punti più alta del dovuto.
Chiaro, non è che ora ogni volta che ci troviamo di fronte ad una statistica dobbiamo calcolare la deviazione standard: lo scopo di questo primo capitolo di “Stats for dummies” sarebbe piuttosto far capire come due numeri apparentemente uguali possano in realtà essere differenti.
Osservare con attenzione i numeri, aiutandosi sempre con il numero di partite giocate (e, nel caso si ritenga opportuno, con la deviazione standard), permette di evitare errori banali che, se non rivelati, portano ad avere analisi errate e forvianti.
Di Luca Cappelletti











 Occorre essere registrati per poter commentare
Occorre essere registrati per poter commentare
